Entradas

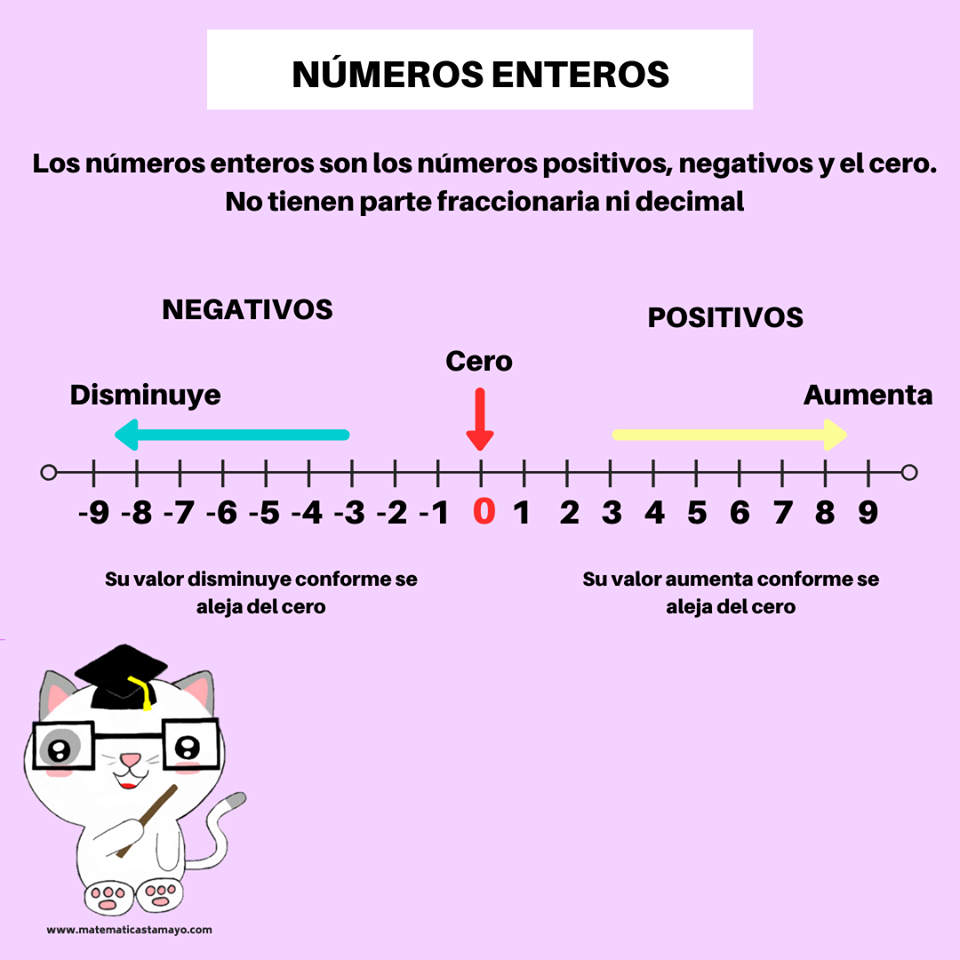
Situaciones problemáticas con números enteros.

Imagen
Matemática                                                                            Lunes 18/05/2020 Situaciones problemáticas con números enteros  Para resolver una situación problemática se deben tener en cuenta los siguientes pasos: Lee despacio el enunciado . Lo más importante es entender el problema por eso tienes que leerlo despacio y las veces que sean necesarias para comprenderlo. Escribe los datos que te brinda el problema y lo que te pide que resuelvas. Haz las operaciones : una vez comprendido y extraídos los datos, tienes que efectuar las operaciones. Exprésalas con claridad indicando que és cada resultado que obtienes. Escribe la solución indicando qué es lo que obtienes y respondiendo con claridad a lo que te pide el problema.  Ejemplo : Leo debe $15. Si su madre le da $60 de paga y se gasta con sus amigos $20, ¿cuánto dinero le queda? ¿Tendrá pendiente alguna deuda?  Paso 1: Leer el enunciado las veces que sean necesarias para comprenderlo. Paso 2:
Publicar un comentario
Leer más

Características de una función: Intersección con los ejes.

Imagen
Características de una función En la gráfica de una función es importante distinguir: las variables que se relacionan, el dominio y la imagen. Además, dónde están ubicados y qué significan: 1- Intersección (corte) con el eje de ordenadas ( ordenada al origen ). 2- Intersección (corte) con el eje de abscisas ( ceros o raíces de la función ). 3-Puntos máximos y/o mínimos relativos: puede tener varios máximos o mínimos relativos y puede coincidir con alguna de las intersecciones con los ejes.  Ceros o raíces de una función. Son los valores de la variable Independiente para los cuales la función corta al eje de las abscisas o eje x .  Los ceros o raíces se calculan igualando la función a cero y despejando x. Ordenada al origen. Se llama así al punto donde la función corta al eje de ordenadas o eje y . ...PRACTICAMOS... Actividad 1: Una pelota de tenis se arroja a un recipiente con agua. El gráfico muestra cómo se ubica ese elemento respecto del nivel
Publicar un comentario
Leer más

Repaso de números enteros

Imagen
Matemática                                                                                            Lunes 04/05/2020 Actividades de repaso: OPERACIONES CON NÚMEROS ENTEROS (SUMAS)     1) Completa las siguientes frases:   Para sumar a un número un entero positivo, movemos el número a la ................. en la ......... .................................. Para sumar a un número un entero negativo, movemos el número a la ................. en la . ...... ..... ................................  Palabras claves: IZQUIERDA - RECTA NUMÉRICA - DERECHA - RECTA NUMÉRICA     2) Con ayuda de la recta numérica realiza las siguientes sumas:           a) (-3) + (+11)                         b) (+4) + (-10)                             c) 0 + (-3)                  d) (+5) + (-12)                         e) (-7) + (+7)                              f) (-14) + (+8)    3)  Relaciona cada suma con su resultado:         (+5) + ( +6)    
Publicar un comentario
Leer más

SUMA Y RESTA DE NÚMEROS ENTEROS.

Imagen
SUMA Y RESTA DE NÚMEROS ENTEROS.  A modo repaso recuerda la ubicación y el ordenamiento de los números enteros en la recta numérica.  Como vimos la clase pasada Sumar números positivos es hacer una suma normal. Ejemplo: 2 + 3 = 5 realmente quiere decir "positivo 2 más positivo 3 es igual a positivo 5". Podrías escribirlo así: (+2) + (+3) = (+5) Restar números positivos Esto es una simple resta. Ejemplo: 6 - 3 = 3 realmente quiere decir "positivo 6 menos positivo 3 es igual a positivo 3". Podrías escribirlo así: (+6) - (+3) = (+3) ¿Pero qué pasa si tenemos números negativos... ? Por ejemplo, ¿cuánto es 6 - (-3)? Restar un negativo es lo mismo que sumar Alexa puede portarse bien o mal en casa. Así es que sus padres le han dicho:  "Si te portas bien te damos 3 puntos (+3). Si te portas mal te quitamos 3 puntos (-3). Cuando llegues a 30 puntos te damos un juguete." Alexa empieza el día con 9 puntos puntos: 
Publicar un comentario
Leer más

CUESTIONARIO. CARACTERÍSTICAS DE UNA FUNCIÓN.

Imagen
Esta gráfica, ¿cuántos máximos relativo tiene?   *                                   5 puntos No tiene 3 5 4 7 Las funciones se pueden representar utilizando tabla de valores, fórmula, gráfica y la forma verbal. La representación en la imagen corresponde a una  * 5 puntos Fórmula. Tabla de valores. Forma verbal. Gráfica. Esta gráfica, ¿cuántos mínimos relativos tiene?  * 5 puntos No tiene 3 7 5 4 Indica los máximos y mínimos relativos de la función:  * 5 puntos Máximos: (-4;4) , (0;0) y (4;4) Mínimos: (-2;-3) y (2;-3)
Publicar un comentario
Leer más